#Building and Construction
Enabling Martian habitability with silica aerogel via the solid-state greenhouse effect
The low temperatures1,2 and high ultraviolet radiation levels3 at the surface of Mars today currently preclude the survival of life anywhere except perhaps in limited subsurface niches4.
Several ideas for making the Martian surface more habitable have been put forward5,6,7,8, but they all involve massive environmental modification that will be well beyond human capability for the foreseeable future9. Here, we present a new approach to this problem. We show that widespread regions of the surface of Mars could be made habitable to photosynthetic life in the future via a solid-state analogue to Earth’s atmospheric greenhouse effect. Specifically, we demonstrate via experiments and modelling that under Martian environmental conditions, a 2–3 cm-thick layer of silica aerogel will simultaneously transmit sufficient visible light for photosynthesis, block hazardous ultraviolet radiation and raise temperatures underneath it permanently to above the melting point of water, without the need for any internal heat source. Placing silica aerogel shields over sufficiently ice-rich regions of the Martian surface could therefore allow photosynthetic life to survive there with minimal subsequent intervention. This regional approach to making Mars habitable is much more achievable than global atmospheric modification. In addition, it can be developed systematically, starting from minimal resources, and can be further tested in extreme environments on Earth today.
Main
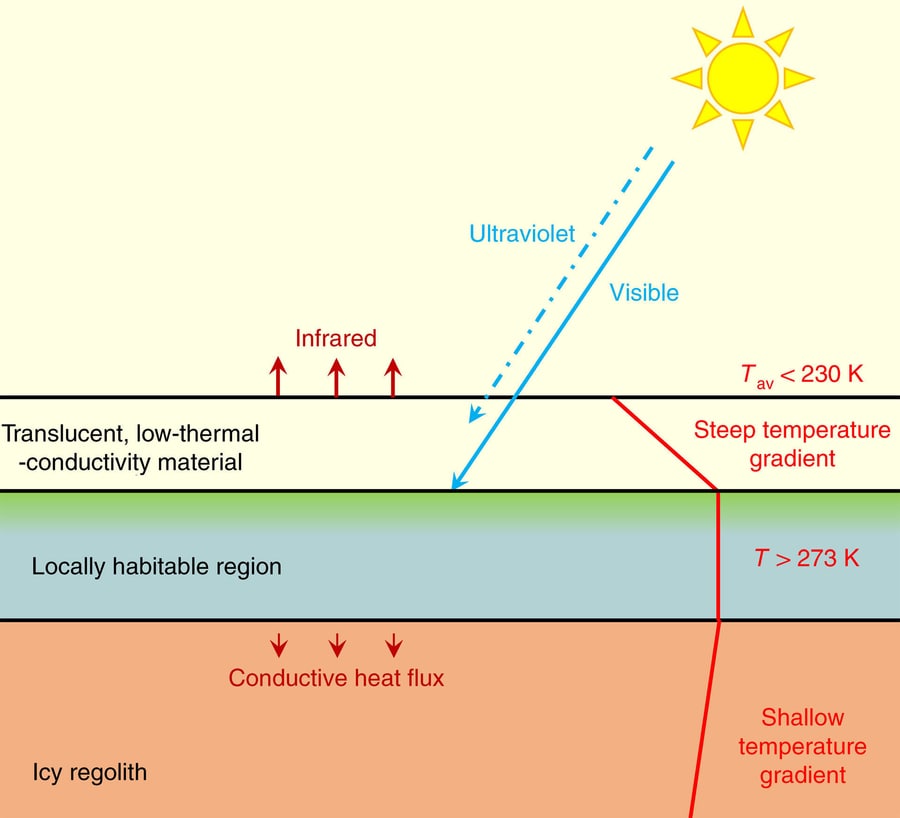
Around 50 K of surface warming is required on Mars to raise annual average low- to mid-latitude temperatures to above the melting point of liquid water. Mars’s current atmosphere is too thin to significantly attenuate ultraviolet (UV) or to provide greenhouse warming of more than a few kelvins. However, observations of dark spots on Mars’s polar carbon dioxide ice caps suggest that they are transiently warmed by a greater amount via a planetary phenomenon known as the solid-state greenhouse effect10,11,12,13, which arises when sunlight becomes absorbed in the interior of translucent snow or ice layers14,15. The solid-state greenhouse effect is strongest in materials that are partially transparent to visible radiation but have low thermal conductivity and low infrared transmissivity (Fig. 1). Although carbon dioxide and water ices are common on Mars, they are much too volatile to make robust solid-state greenhouse shields for life. Silica has more favourable properties in that it is chemically stable and refractory at Martian surface temperatures. Solid silica is transparent to visible radiation, but opaque to UV at wavelengths shorter than 200–400 nm and to infrared at wavelengths longer than ~2 μm, depending on the abundance of impurities such as hydroxy groups. However, the thermal conductivity of solid silica (0.8–1.6 W m−1 K−1) (ref. 16) is too high to allow a strong warming effect.
Silica aerogels, which consist of nanoscale networks of interconnecting silica clusters, are over 97% air by volume and have some of the lowest measured thermal conductivities of any known material (~0.02 W m−1 K−1 at 1 bar pressure or 0.01 W m−1 K−1 at Martian atmospheric pressures)17. Because of these properties, silica aerogels have gained prominence in many fields of engineering, including in the design of passively heated buildings on Earth18 and even in the Mars Exploration Rovers, where thin aerogel layers were used to provide night-time thermal insulation19. Silica aerogels therefore hold excellent potential for creating strong solid-state greenhouse warming under Martian conditions.
We performed experiments to demonstrate the warming potential of silica aerogel solid-state greenhouse layers under Mars-like insolation levels. Our experimental set-up consists of a layer of silica aerogel particles or tiles (see Fig. 2) on a low-reflectivity base surrounded by thermally insulating material (see Methods). The apparatus is exposed to visible radiation from a solar simulator. The broadband flux incident on the layer is measured with a pyranometer, and temperature is recorded by calibrated glass-bead thermistors.
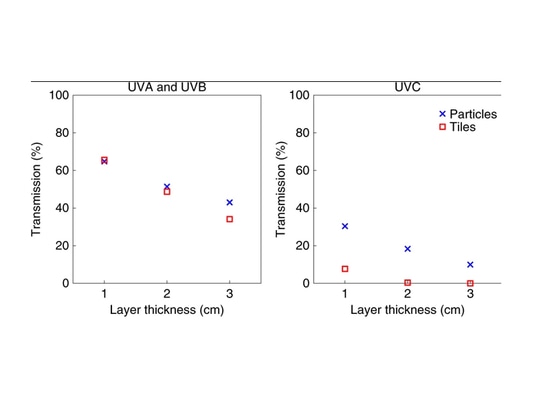
Figure 3 shows the experimental results for both aerogel particle and tile layers versus received visible flux in the 100–200 W m−2 range. For comparison, Earth’s global mean received flux is 342 W m−2, while that of Mars is 147 W m−2. As can be seen, temperature differences of over 45 K are achieved for aerogel particle layers of 3 cm thickness receiving a flux of 150 W m−2. Aerogel tiles, which have higher visible transmission, cause temperature differences that are ~10 K higher, reaching >50 K at just 2 cm thickness. Our experimental results show that under Mars-like insolation levels, warming to the melting point of liquid water or higher can be obtained under a 2–3 cm-thick silica aerogel layer. The peak obtainable warming is likely even higher (see Methods), because heat is lost in our experimental set-up via sidewall and base thermal losses and convection. We also measured the transmission of the aerogel particles and tiles in the UV and found strong attenuation of UVA and UVB (280–400 nm) and near-total attenuation of the most hazardous UVC (220–275 nm) radiation (Fig. 4).
Although raising surface temperatures and blocking UV radiation are the two most critical considerations for permitting life to survive on Mars, additional constraints due to atmospheric pressure, nutrient availability and dust deposition also need to be considered. Brines can remain liquid below the freezing point of pure water, which could lower the temperature requirement below the 273 K we have assumed here20, although for high enough salinities, habitability would become restricted to halophilic organisms only. The higher carbon dioxide partial pressure on Mars versus Earth is favourable for plant growth6, but the low total atmospheric pressure means that at temperatures of 273 K or higher, the undersides of silica aerogel greenhouse shields would need to remain slightly pressurized relative to the atmosphere to avoid loss of water vapour either vertically or laterally. This would place light demands on their structural properties, which could plausibly be met by interspersing the silica aerogel with thin layers of solid transparent material or via organic polymer reinforcement21,22. Most nutrients appear to be readily available on the Martian surface, with the abundances of some (such as iron and sulfur) higher than on Earth23. The low partial pressure of N2 on Mars may pose a challenge for nitrogen fixation by unadapted terrestrial microorganisms. However, nitrate deposits, which have been observed in situ on the surface of Mars, are a plausible alternative source of nitrogen24.
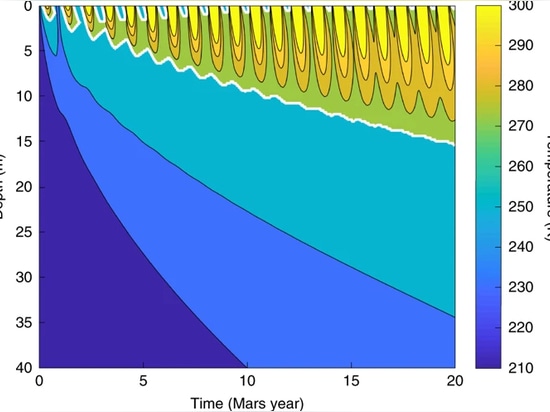
The most favourable locations on Mars for creating local life-supporting regions are those that combine the key resources of light and surface water while minimizing hazards such as excessive dust deposition. Within the latitude band where solar flux is high throughout the year (45° S–45° N), there are many mid-latitude locations where observations indicate the presence of near-surface ground ice25,26,27 and climate model simulations28 indicate dust accumulation rates should be low. Figure 4 shows the results of a coupled radiative–thermal calculation for the evolution of Martian subsurface temperatures at one such location (Deuteronilus Mensae) in the presence of a solid-state greenhouse silica aerogel layer. Our model takes into account changes in Martian insolation and aerogel radiative transfer, thermal conduction in both the aerogel and the regolith and the latent heat associated with melting/freezing of regolith ice (see Methods). As can be seen in Fig. 5, assuming the presence of a 2.5 cm-thick aerogel layer, subsurface temperatures down to depths of several metres are high enough to allow liquid water throughout the Martian year after a few years at this location.
Our results show that via the solid-state greenhouse effect, regions on the surface of Mars could be modified in the future to allow life to survive there with much less infrastructure or maintenance than via other approaches. The creation of permanently warm regions would have many benefits for future human activity on Mars, as well as being of fundamental interest for astrobiological experiments and as a potential means to facilitate life-detection efforts29. The solid-state greenhouse warming concept also has applications for research in hostile environments on Earth today, such as Antarctica and Chile’s Atacama Desert.
In future work, it will be important to investigate the ease with which traditional silica aerogel manufacturing techniques17 can be adapted to conditions on Mars. However, given the ability of life on Earth to modify its environment, it is also interesting to consider the extent to which organisms could eventually contribute to sustaining Martian habitable conditions themselves. On Earth, multiple organisms already exist that utilize silica as a building material, including hexactinellid sponges and diatom phytoplankton30,31. Diatoms in particular can grow up to several millimetres in length, produce frustules from ~1–10 nm-diameter amorphous silica particles (smaller than the mean pore diameter in silica aerogel networks)17,32 and are already known to have high potential for bionanotechnology applications in other areas31,33. It could therefore be interesting in the future to investigate whether high-visible-transmissivity, low-thermal-conductivity silica layers could be produced directly via a synthetic-biology approach. If this is possible, in combination with the results described here, it could eventually allow the development of a self-sustaining biosphere on Mars.
As there is the potential for Mars to be made habitable to photosynthetic life in the near to medium term, important ethical and philosophical questions must be considered. Most obviously, if Mars still possesses extant life today, its survival or detection might be hampered by the presence of Earth-based microorganisms34. However, no mission has yet detected life on Mars, so if it does exist, it is likely to be confined to very specific regions in the subsurface. The approach studied here would not result in the survival of Earth-based life outside solid-state greenhouse regions, so it should be unlikely to pose a greater risk to the search for Martian life than the presence of humans on the surface. Nonetheless, the planetary protection concerns surrounding the transfer of Earth-based life to Mars are important, so the astrobiological risks associated with this approach to enabling Martian habitability will need to be weighed carefully against the benefits to Mars science and human exploration in future.
Methods
Experimental
Our experimental set-up consisted of an 18 cm × 18 cm solid-state greenhouse layer of variable thickness surrounded by polystyrene for insulation, with a solar simulator positioned above the layer to provide varying levels of visible irradiance (Supplementary Fig. 1). For the solid-state greenhouse layer, we used combinations of silica aerogel particles (radii between 700 μm and 4 mm; Lumira, Cabot Aerogel) and tiles (10 cm × 10 cm × 1 cm; Large Hydrophobic Silica Tiles, Tiem Factory). In the particle experiments, the entire layer was filled with particles, while in the tile experiments, the tiles were placed in the centre and the remaining volume was filled with particles. Shallow-pile black felt of visible albedo <0.01 (Protostar flocked light trap material) was placed below the aerogel layer to maximize the absorption of incoming visible radiation from the solar simulator.
Temperature data were collected via an array of compact (0.8 mm diameter) negative-temperature-coefficient thermistors. The thermistors were calibrated versus a reference digital thermometer (Traceable Model 1235D30) between 0 °C and 100 °C by suspending them in a continuously stirred water bath and recording the thermometer reading and thermistor resistance simultaneously. A least-squares fit was then used to determine resistance as a function of temperature according to the formula
R=C(TT0)β
(1)
where R is resistance in kilo-ohms, T is temperature in kelvins, T0 = 273.15 K is a reference temperature, and C and β are calibration constants. Calibration results and best-fit values for C and β are shown in Supplementary Fig. 2. We also tested the difference in resistance between individual thermistors at the same temperature and found it to be minimal compared with other error sources in the temperature range of interest. Thermistors were attached to the base, top and exterior of the solid-state greenhouse apparatus and connected to a voltage divider circuit connected to a multiplexer/ESP8266 microcontroller for data acquisition. We also used a small thermal camera (Seek Thermal Imager) as an additional check on temperature data recorded by the thermistors and to diagnose side and base regions of elevated heat flux during the experimental set-up.
Visible illumination to simulate the solar flux was provided by a 250 W protected pulse-start metal-halide lamp. A metal-halide light source was chosen because it approximates the zero-air-mass (AM0) solar spectrum more closely at most wavelengths than other light sources such as xenon arc35 at a lower cost and reduced explosion risk. The lamp was encased in a fan-cooled light box with mirrored ceiling and black sidewalls, to maximize the transmission of well-collimated light to the aerogel layer (Supplementary Fig. 1). A glass shield was placed between the lamp and experiment as a precaution against explosive lamp failure. The percentage of solar flux occurring above the wavelengths at which glass begins to absorb significantly (2–3 μm) is of the order of a few percent, so absorption of near-infrared radiation by the shield was not judged to be a significant source of error in our results. The optical properties of silica aerogel do not vary significantly across the visible wavelength range36, so the relatively small differences between the metal-halide lamp spectrum and the solar spectrum incident at Mars’s surface were not a significant source of uncertainty in our results either. The lamp was positioned between 20 cm and 30 cm above the silica aerogel sample. A laboratory jack was used to perform adjustments to the aerogel layer and pyranometer height to vary the received radiant flux. All experiments were run until thermal equilibrium was reached, which was judged by observing the value and rate of change of temperature at the base and top of the silica aerogel layer. Typically, this took ~2 h for each experiment. Experiments were performed at ambient pressure and a background temperature of 298 ± 1 K.
The broadband visible fluxes incident on the sample were measured using a first-class double glass dome pyranometer (Hukseflux Instruments model SR-11). The SR-11 model used had a sensitivity of 14.22 × 10−6 ± 0.15 V per W m−2 and hence a ±1% calibration error. The estimated hourly uncertainty at equatorial latitudes during field observations stated in the pyranometer’s technical literature was ±3.1%, which is the value we used when stating our flux measurement uncertainties (see Supplementary Fig. 3). Spatial variation of the incident flux was recorded by moving the pyranometer across a 0.15 m × 0.15 m grid in 3 cm intervals (Supplementary Fig. 4). Temporal variability of the flux was also measured and found to be <2% over a 2 h interval (Supplementary Fig. 4). The UV transmission experiments were performed using a compact 4 W UV lamp with dual tubes to emit radiation peaking in either the 365 nm (UVA and UVB) or 254 nm (UVC) range. For UV measurement (see Supplementary Table 1), we used calibration-certified Sper Scientific UVA, UVB and UVC detectors, which had a quoted accuracy of ±4%. The UVA and UVB detector had peak sensitivity in the 350–360 nm range, with the calibration point at 365 nm, while the UVC detector had peak sensitivity at 255–265 nm, with the calibration point at 254 nm.
Temperature error analysis
For the temperature difference measurement, we considered errors from four sources: the data-acquisition digitization error, the uncertainty in the voltage divider resistance and the errors in the calibration parameters C and β. The digitization error was 3.3 V/210 = 3.2 mV, given the ten-bit data-acquisition system used, or 3.2 mV, while the voltage divider resistance error was 1%, or 0.1 kΩ for the 10 kΩ resistor. The errors in C and β were calculated from the log-linear least-squares fit and are shown in Supplementary Fig. 2.
From equation (1) and the voltage divider equation, the temperature difference between the base and top of the aerogel layer is
ΔT(Vb,Va)=T(Vb)−T(Va)=T0[(R1,bVbC(V0−Vb))1/β−(R1,aVaC(V0−Va))1/β]
(2)
where V0 = 3.3 V is the peak voltage, T(Va) is the top-of-layer temperature, T(Vb) is the base temperature and Vi and R1,i correspond respectively to the output voltage and divider circuit fixed resistance for location i. We propagated uncertainties in Va, R1,a, Vb, R1,b, C and β via a Taylor expansion, assuming small uncertainties37. The resulting estimated uncertainties in ΔT, which were used to produce the error bars in Fig. 3, are shown in Supplementary Fig. 5.
Theory and numerical analysis
Extreme upper limit of solid-state greenhouse warming potential
An idealized upper limit to solid-state greenhouse warming can be derived by considering a material with zero thermal conductivity that is perfectly transparent below some cut-off wavelength λc, but absorbing at longer wavelengths. Under these circumstances, cooling can occur only via radiation from the base of the layer in the visible, and the base energy balance becomes
π∫0λcBλ[T]dλ=Fb
(3)
where λ is the wavelength, Bλ[T] is the Planck spectral irradiance, T is the base temperature and Fb is the visible radiation (at wavelengths shorter than λc) absorbed at the layer base. Given the standard definition for Bλ[T], equation (3) can be solved by a root-finding approach. The annual global mean solar flux received by Mars is ~150 W m−2. Given λc = 2 μm and Fb = 150 W m−2, equation (3) yields T = 721 K, which is close to the surface temperature of Venus. Shifting λc to smaller values would lead to even higher T values, with the temperature achieved asymptoting to the solar spectrum effective blackbody temperature as λc → 0.
Optimal thickness of a solid-state greenhouse layer
More realistically, we can determine the thickness required for a solid-state greenhouse layer to maximize surface temperature when its extinction optical depth in the visible is non-negligible, as is the case for all real materials. Here, we neglect three-dimensional and basal conduction effects and assume constant thermal conductivity. We also assume that the solid-state greenhouse layer effectively absorbs infrared radiation such that conduction is the dominant mode of heat transport in the layer. This analysis builds on previous theoretical studies of the solid-state greenhouse effect in snow and ice12,15,38.
If the solid-state greenhouse layer has a non-zero extinction coefficient in the visible, Fb will depend on h, the total layer thickness. Then, the total warming will depend on a balance between the attenuation of visible radiation and the thermal insulation provided by the layer. From the thermal diffusion equation, the steady-state temperature gradient inside the layer is39
dTdz=−Fb(h)κ
(4)
where κ is the solid-state greenhouse layer thermal conductivity and z is the height in the layer. Integrating from 0 to h yields
ΔT=Tb−Ta=Fb(h)hκ
(5)
where Tb and Ta are the temperatures at the base and top of the layer, respectively. To find the peak temperature difference as a function of h, we differentiate to obtain
dΔTdh=Fb(h)′hκ+Fb(h)κ
(6)
We then set dΔT/dh to zero, yielding Fb(h)′h = −Fb(h) (here the prime on Fb(h) indicates differentiation with respect to h). Now, if
Fb(h)=Fae−τ(h)/μ¯¯¯=Fae−αh/μ¯¯¯
(7)
where Fa is the incident solar flux on the layer, τ is the layer vertical path extinction optical depth, α is the layer extinction coefficient in the visible and μ¯ is the mean solar zenith angle cosine, it immediately follows that the optical depth for maximum warming τm is τm/μ¯=1 and the optimal layer height hm is
hm=μ¯/α
(8)
Assuming vertical path transmission values of T=e−τ=0.8 and 0.6 for the 1 cm-thick silica aerogel tile/particle layers, respectively, we find α = 22.3 m−1 and 51.1 m−1, or hm = 4.5 cm and 2.0 cm, given μ¯=1. The latter value is reasonably close to the layer depth of maximum warming achieved in the aerogel particle case (see Fig. 3), with the slight difference probably due to multiple scattering effects. From equation (5), the theoretical maximum temperature difference is simply
ΔTm=μ¯Fae−1ακ
(9)
Given Fa = 150 W m−2 and κ = 0.02 W m−1 K−1, ΔTm = 124 K for the tiles and ΔTm = 54 K for the particles. The temperature differences achieved in our experiments were lower than this because we used aerogel layer thicknesses of up to 3 cm only and losses from convection and sidewall and base conduction were non-negligible in our relatively small apparatus.
One-dimensional numerical model of solid-state greenhouse warming on Mars
Our numerical model of the solid-state greenhouse effect on Mars calculates the diurnal average radiative transfer of the aerogel layer, the transport of heat via diffusion in the underlying regolith and the solar zenith angle as a function of time and location. Downwelling solar radiation and thermal radiation from the Martian atmosphere are calculated using data from the Mars Climate Database (MCD) version 5.3 Climatology scenario (http://www-mars.lmd.jussieu.fr/mars/access.html)2. The solar zenith angle model is similar to that described in ref. 40 (see also ref. 39), with the Martian orbital obliquity, eccentricity and season angle of perihelion taken into account via the method described in ref. 41, and the season angle linked to time via Kepler’s equation42. Our model output was validated under standard Martian conditions versus figure 1 of ref. 43 and by comparison with MCD results.
Subsurface heat transport occurs in the model via thermal diffusion according to
chρ∂T∂t=∂∂z(κr∂∂zT)+q(z)
(10)
Here, z is depth, κr is the regolith thermal conductivity, ch is heat capacity, ρ is density and q is the local heating rate due to latent heat effects. We solve equation (10) via a centred difference in the spatial domain and explicit forward-stepping in time.
Our model domain extends from the surface down to 80 m depth, and we integrate over a time period of 15 Martian years (Supplementary Table 2). We neglect horizontal heat losses, so our model is appropriate for a set-up where the horizontal extent of the solid-state greenhouse layer is tens of metres or more in both directions. As the solid-state greenhouse layer is only a few centimetres thick, we assume that it is in thermal equilibrium at every time step. The thermal balance at the top of the layer is taken to be
σT4a−FIR=F1=κTb−Tah
(11)
where FIR is the downwelling thermal radiation from the Martian atmosphere (supplied from the MCD), Tb is the temperature immediately underneath the layer and κ and h are defined as in equation (4). This approach neglects additional heating or cooling of the surface due to sensible or latent atmospheric effects, which are of secondary importance due to the low density of Mars’s atmosphere12. This equation is solved for Ta via a root-finding method at every time step. The solid-state greenhouse layer thermal conductivity is taken to be 0.01 W m−1 K−1, which is an appropriate value for silica aerogel thermal conductivity given atmospheric pressures under 0.1 bar (ref. 17). The temperature immediately underneath the solid-state greenhouse layer is then evolved according to
chρ∂Tb∂t=(F2+Fabs−F1)/Δz
(12)
Here, F2 is the conductive heat flux from the layer below, Δz is the subsurface numerical discretization thickness and Fabs is the absorbed solar flux. The absorbed solar flux is modelled as
Fabs=Fsole−τ/μ¯(t,λ)
(13)
Here, Fsol is the diurnal mean solar flux at the surface of Mars (supplied from the MCD) and μ¯(t,λ) is the diurnal mean solar zenith angle cosine output from the insolation model at time t and latitude λ. Finally, τ = αh is the solid-state greenhouse layer vertical path extinction optical depth, as in our previous analysis. We conservatively neglect the diffuse visible flux to the layer base due to multiple scattering effects.
The initial surface temperature in our simulation is taken to be the annual mean surface temperature in that location, on the basis of MCD results. The initial regolith temperature gradient is set to the Martian geotherm, which we take to be 15 K km−1 on the basis of an assumed geothermal heat flux of Fgeo = 30 mW m−2 and mean regolith conductivity of 2 W m−1 K−1, following ref. 44. At the bottom boundary, we assume a fixed heat flux equal to Fgeo.
We assume the regolith to be porous and saturated with ice, with the ice volume mixing ratio set to 0.5, corresponding to an ice-rich mid-latitude region such as Deuteronilus Mensae. Regolith density and sensible heat capacity were set by taking a weighted average of basalt and water ice. We found fairly low sensitivity of our results to the assumed ice/rock ratio. We take the latent heat during ice freezing and water melting into account in the thermal calculation by tracking the concentration of ice and water at each level through time, in a similar way to ref. 12. We then force the temperature to remain at or below 273.15 K whenever heat is entering a given layer and ice is still present, and assume that this heat is entirely used to melt the ice. Similar constraints are applied for the freezing of liquid water under cooling conditions. Our numerical model has been validated versus an analytic solution (propagation of a Gaussian pulse) and verified to conserve energy and total H2O mass globally to machine precision at every time step.